Измерение силы связи между номинальными переменными

В условиях, когда связь значима и величина значимости (Significance) близка к нулю, появляется необходимость оценить силу этой связи и выявить наиболее связанные переменные. Непосредственное использование коэффициента Xи-квадрат неудобно - он зависит от числа объектов, из-за чего одинаковые по пропорциям распределений таблицы на выборках разного объема будут оценены по-разному.

Коэффициент Пирсона PHI=

- лишен этого недостатка, но дипазн его изменения зависит от размерности таблиц:

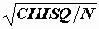
Более устойчив к размерности выборки коэффициент контингенции:

, 0
CC<1;

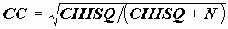
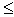
еще лучше в этом отношении коэффициент Крамера

, где к=min[r,c],

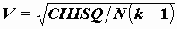
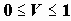
Все эти коэффициенты можно использовать для оценки силы связи и, сравнивая их по величине, делать вывод о более тесной или менее тесной связи. Эти коэффициенты не носят точного характера - поэтому их использование - дело вкуса каждого исследователя.

Заметим, что коэффициенты анализа связи переменных "хи-квадрат" (CHISQ), "фи" (PHI) и обычный коэффициент корреляции изобретены Пирсоном.

Содержание раздела