Определение нелинейного уравнения
Нелинейное уравнение с одним неизвестным можно записать в виде:
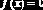
Совокупность значений переменной

этого уравнения, а каждое значение

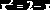
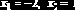
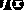

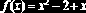
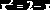
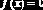
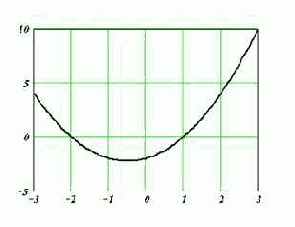
Рис. 8.1.1. К определению корней нелинейного уравнения
Если в запись уравнения входят только алгебраические функции (четыре арифметические операции и возведение в степень), то уравнение называется алгебраическим, и оно после необходимых преобразований может быть записано в виде:
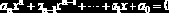
Числа
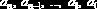
Известно, что уравнение (8.1.2)


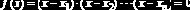
где
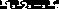
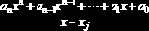
будет на единицу меньше, и среди его корней не будет корня

Нелинейное уравнение, в которое входят трансцендентные
функции (показательные, логарифмические, тригонометрические и обратные тригонометрические функции), называется трансцендентным. Примером может служить уравнение
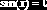
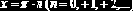
Решение уравнения можно найти, используя различные методы: аналитические (корни определяются аналитическим выражением), графические (приближенные значения корней находятся из графика – пример рис. 8.1.1), численные (приближенные численные значения корней определяются в результате некоторой вычислительной процедуры). В дальнейшем будут рассматриваться только численные методы.
Вычисление корней численными методами включает два основных этапа:
- отделение корней;
- уточнение корней до заданной точности.
Рассмотрим эти два этапа подробно.